核心原理:相位法测距
相位式测距的本质不是直接测量时间,而是通过测量激光光波往返后产生的相位差来间接计算距离。
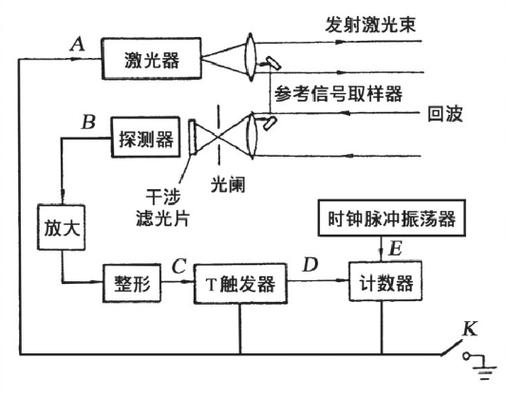
我们可以用一个简单的比喻来理解: 想象你向远处的一个目标匀速扔出一个带有标记的球(激光脉冲),并记录下球离开你时的“相位”(球上有一个红点,初始时红点朝上),球到达目标后反射回来,你接住它,并再次观察球上红点的“相位”,由于球在飞行过程中一直在自转(相当于光波在传播),返回时红点的朝向可能已经改变了,这个“朝向的改变量”就是相位差。
知道了球的自转速度(光速)和飞行一圈(一个波长)所需的时间,你就可以通过相位差换算出球飞了多远,从而计算出目标的距离。
数学原理推导:
-
基本公式:激光从发射到被接收,往返传播的距离
D_total与相位差 的关系为:D_total = (c / f) * (Δφ / 2π)c:光速 (≈ 3×10⁸ m/s)f:激光的调制频率(Hz)- 激光往返产生的总相位差(弧度)
-
往返距离与单程距离:往返距离
D_total是单程距离D的两倍,即D_total = 2D,代入上式:2D = (c / f) * (Δφ / 2π) (图片来源网络,侵删)
(图片来源网络,侵删) -
波长引入:我们知道,波长
λ = c / f,公式可以简化为:2D = λ * (Δφ / 2π) -
整数倍波长与余数:相位差 是一个周期性变化的量,它总是
2π的整数倍加上一个小于2π的余数,我们通常将相位差表示为:Δφ = 2π * N + Δφ'N:相位差中包含的完整周期数(整数,未知)。- 相位差中不足一个完整周期的部分(可精确测量)。
-
最终公式:将 代入公式,得到距离
D的最终表达式:D = (λ / 2) * (N + Δφ' / 2π)λ / 2(半波长):这是相位式测距中一个至关重要的概念,被称为“测距尺”或“单位长度”,它决定了测距的量程和精度。- 量程:由于
N是未知整数,理论上只要相位差 不超过2π,系统就无法区分N的值。最大不模糊测程(Unambiguous Range)就是半波长λ / 2,一旦距离超过λ / 2, 就会开始重复,导致距离出现“多值性”或“模糊”。 - 精度:测距的精度取决于对相位差 的测量精度,通常可以达到
λ / 100甚至更高。调制频率越高(波长越短),测距精度越高,但最大不模糊测程越小。
- 量程:由于
系统组成
一个典型的相位激光测距系统主要由以下几个部分组成:
-
激光器:
- 产生一束连续的、相干性极好的激光(通常是He-Ne激光器、半导体激光器等)。
- 在现代系统中,也常用直接调制的半导体激光器。
-
调制器:
- 核心部件,它将来自激光器的连续激光波的振幅、频率或相位进行周期性变化(调制)。
- 最常用的是正弦波调制,将激光强度按照
I(t) = I₀ * (1 + m * sin(2πft))的规律变化,f就是调制频率。 - 调制后的激光波就携带了特定的频率信息,成为“测距信号”。
-
发射光学系统:
- 通常包括一个准直透镜,将经过调制的激光束发散角压缩,形成一束细而平行的光束,射向远处的目标。
-
接收光学系统:
- 通常是一个接收望远镜,用于收集从目标反射回来的微弱激光信号,并将其聚焦到光电探测器上。
-
光电探测器:
- 核心是光电二极管或雪崩光电二极管。
- 它的作用是将接收到的光信号(强度变化)转换成相应的电信号(电压或电流变化),这个电信号的相位与返回的激光信号的相位相对应。
-
信号处理与解调单元:
- 这是系统的“大脑”,负责核心的测距计算。
- 混频/鉴相:将探测器接收到的微弱信号与一个从调制器引出的原始参考信号进行混频(相乘),然后通过低通滤波器,这个过程可以滤除高频载波,得到一个只包含相位差的低频信号。
- 相位差测量:使用高精度的相位计(如基于过零检测、相关算法或FFT的数字信号处理器)来精确测量参考信号和接收信号之间的相位差 。
- 计算与控制:根据测得的 和已知的
λ / 2,计算出距离D,为了解决N的模糊度问题,系统通常会采用多频率测距法(见下文)。
-
时钟与控制单元:
为整个系统提供稳定的时钟信号,控制调制器的频率,并协调各个模块的工作。
关键技术:解决距离模糊度
如前所述,单频测距的最大量程受限于半波长 λ / 2,为了实现远距离、高精度的测量,必须解决距离模糊度问题,最常用的方法是多频率测距法,类似于用多个不同长度的“尺子”去测量一个很长的物体。
-
基本思想:采用两个或多个不同的调制频率
f₁和f₂(对应不同的测距尺U₁ = λ₁/2和U₂ = λ₂/2)进行测量。- 用高频
f₁(短尺U₁)进行测量,得到一个高精度但可能存在模糊的粗测结果D₁。 - 用低频
f₂(长尺U₂)进行测量,得到一个低精度但量程足够、无模糊的粗测结果D₂。 U₂必须大于U₁,U₂是U₁的整数倍关系效果最佳。
- 用高频
-
解算过程:
- 系统首先用长尺
U₂测量,得到一个在[0, U₂)范围内的距离值D₂,这个值确定了距离所在的“大区间”。 - 然后系统用短尺
U₁进行高精度测量,得到D₁。 - 将
D₂和D₁结合起来,通过计算(如解同余方程)得到唯一的、高精度的最终距离值D。 - 类比:这就像先用一把1米长的尺子(长尺)量出房间长度是“12米多”,再用一把1厘米长的尺子(短尺)精确量出是“12.34米”,多频率法就是用数学方法完成这个过程。
- 系统首先用长尺
优缺点分析
优点:
- 高精度:在中等距离上,精度可达毫米级甚至亚毫米级,远高于脉冲式测距。
- 高分辨率:对距离变化的分辨能力非常强。
- 抗干扰能力强:通过调制和解调,可以有效滤除背景光和电噪声的干扰。
缺点:
- 最大测程受限:单频测距存在明显的距离模糊问题,需要复杂的解算。
- 对合作目标要求高:在漫反射表面(如墙面、岩石)上,信号会严重衰减和展宽,导致信噪比下降,精度急剧降低,通常需要使用角反射器作为合作目标,以最大限度地反射激光信号。
- 系统复杂,成本较高:相比简单的脉冲测距模块,其电路和光学系统更复杂,价格也更贵。
- 测量速度相对较慢:需要进行多次不同频率的调制和测量,解算过程也需要时间,因此单次测量时间通常比脉冲式长。
应用领域
- 大地测量与工程测绘:高精度控制网布设、大坝、桥梁、隧道等建筑物的变形监测。
- 工业自动化与机器人:机器人定位与导航、精密零件尺寸测量、自动化生产线上的工件定位。
- 军事领域:坦克、火炮的测距系统,精确制导武器的辅助导航。
- 林业与地形测绘:机载或车载激光雷达,结合GPS和IMU,快速生成高精度的数字高程模型。
- 建筑与BIM:对建筑物进行三维扫描和建模。
相位激光测距技术是一种通过测量调制激光往返相位差来实现高精度距离测量的方法,其核心在于利用“测距尺”(半波长)的概念,精度与尺子长度成反比,量程则受限于尺子长度,为了兼顾精度和量程,系统采用多频率法来解决距离模糊问题,尽管系统复杂且对目标有要求,但其卓越的测量精度使其在众多对精度要求苛刻的领域中成为不可或缺的技术。