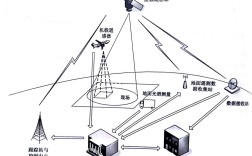
核心原理：多普勒效应
我们必须理解多普勒效应。
- 定义：当波源和观察者之间发生相对运动时，观察者接收到的波的频率与波源发出的频率不同，如果两者相互靠近，接收频率升高；如果两者相互远离，接收频率降低。
- 数学表达式：
对于相对速度为
v的运动，接收频率f_r与源频率f_t的关系为：f_r = f_t * (c + v_r) / (c + v_s)c是波速（电磁波为光速）。v_r是接收者相对于介质的运动速度（朝向源为正）。v_s是源相对于介质的运动速度（朝向接收者为正）。
在定位场景中,通常假设接收机静止，只有辐射源在运动，多普勒频移量 Δf 可以简化为：
Δf = f_r - f_t ≈ (v / c) * f_t * cos(θ)
是辐射源运动方向与辐射源到接收机连线的夹角。
这个公式是整个技术的基础,它告诉我们：
- 频移量
Δf与相对速度v成正比。 - 频移量
Δf与源频率f_t成正比。 - 频移量
Δf与角度 的余弦成正比，即与运动方向有关。
定位基本原理
单台接收机只能测量到一个多普勒频移量,但它无法确定辐射源的具体位置，因为一个频移值可以对应无数个位于不同位置的、以特定速度和方向运动的辐射源。
多普勒频差定位至少需要两台（或多台）接收机。
定位几何模型
假设我们有两台接收机,分别位于 R1 和 R2，一个辐射源 T 以速度 v 运动。
-
测量频率差：
- 接收机
R1测量到的多普勒频移为Δf1。 - 接收机
R2测量到的多普勒频移为Δf2。 - 我们可以计算出两台接收机之间的多普勒频率差：
Δf_diff = Δf1 - Δf2。
- 接收机
-
建立方程： 根据上面的多普勒频移公式，我们有：
Δf1 = (v / c) * f_t * cos(θ1)Δf2 = (v / c) * f_t * cos(θ2)θ1和θ2分别是辐射源运动方向与T->R1和T->R2连线的夹角。两式相减得到频率差方程：
Δf_diff = (v / c) * f_t * (cos(θ1) - cos(θ2))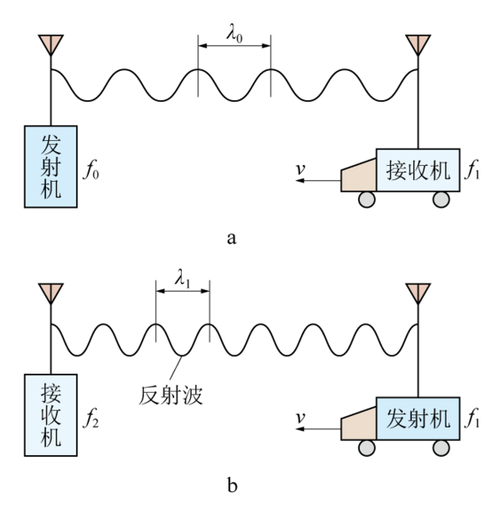
（图片来源网络，侵删） -
定位线（等频差线）： 这个方程看起来很复杂，但我们可以进行变换，根据余弦定理和几何关系，可以推导出一个关键结论： 对于给定的辐射源速度
v和方向，满足Δf1 - Δf2 = 常数的辐射源T的轨迹，是一条以R1和R2为焦点的双曲线。- 这条双曲线就是等频差线，在双曲线上的任何一点，其运动速度和方向如果满足条件，都会导致两台接收机测量到相同的频率差。
-
交点定位：
- 如果我们部署三台接收机（
R1,R2,R3），就可以形成三对组合：(R1,R2),(R1,R3),(R2,R3)。 - 每一对组合都可以测量出一个多普勒频率差,从而确定一条双曲线。
- 这三条双曲线通常会在一个点上相交,这个交点就是辐射源
T的估计位置。
- 如果我们部署三台接收机（
多普勒频差定位就是通过测量不同接收机对之间的频率差，来绘制出多条双曲线，然后通过这些双曲线的交点来确定目标的位置。
技术流程与步骤
- 系统部署：在已知位置部署至少三台（通常更多）接收机，组成一个接收机阵列。
- 信号接收：所有接收机同时接收来自目标辐射源的信号。
- 频率测量：各接收机精确测量接收信号的频率，并计算出相对于已知源频率（或基准频率）的多普勒频移
Δf。 - 计算频率差：系统中心处理单元根据各接收机的测量结果，计算所有接收机对之间的多普勒频率差
Δf_diff。 - 定位解算：
- 建立方程组：根据接收机的几何位置和测量的频率差，建立一组非线性方程。
- 求解：使用最小二乘法、牛顿迭代法等优化算法求解这个方程组，计算出辐射源的位置坐标
(x, y)。 - 运动参数估计：如果还需要估计辐射源的速度和方向，则需要更复杂的模型和更多的观测数据，通常需要多个时间点的连续测量。
- 输出结果：输出辐射源的估计位置、速度、航向等信息。
优点与缺点
优点
- 无源定位：自身不发射信号，只接收目标信号，隐蔽性好，不易被目标察觉和干扰。
- 作用距离远：主要依赖信号的接收强度，只要信号能被接收到，理论上定位距离可以很远。
- 定位精度高：在理想情况下，只要接收机基线足够长，且目标运动速度较快，定位精度可以非常高，甚至能达到米级。
- 抗干扰能力强：对信号本身的调制方式不敏感，只要能稳定提取载波频率即可。
缺点
- 依赖目标运动：这是最核心的限制，如果辐射源是静止的，多普勒频移为零，该技术完全失效，目标运动速度越快，定位效果越好。
- 对同步要求高：所有接收机之间的时间同步必须非常精确（纳秒级），因为频率差的测量对时间抖动极其敏感。
- 计算复杂：定位解算是一个非线性优化问题，计算量较大，对处理单元的性能有一定要求。
- 需要已知源频率：必须精确知道辐射源的发射频率
f_t，否则无法正确计算频移。 - 几何构型影响大：接收机的布阵方式（几何构型）对定位精度影响巨大，当目标位于接收机阵列的对称轴上时，定位误差会急剧增大（称为“几何稀释精度”问题）。
应用场景
-
电子战：
- 辐射源定位：对敌方雷达、通信电台、导弹遥测信号等进行精确定位，为干扰或打击提供目标指示。
- 无源侦察：在不暴露自身的情况下，监视和识别敌方的电磁信号活动。
-
无线电监测：
- 非法电台/信号查找：快速查找和定位未经许可的广播电台、干扰源等。
- 频谱管理：对无线电频谱使用情况进行监测和管理。
-
航空航天：
- 卫星跟踪：跟踪低轨卫星的空间飞行轨迹。
- 弹道导弹预警：通过监测导弹遥测信号的多普勒频差来估算其弹道和落点。
-
民用领域：
- 野生动物追踪：佩戴有无线电发射器的动物，通过固定接收机网络进行追踪。
- 车辆定位：在特定场景下（如车队），通过车辆发射的无线电信号进行相对定位。
与其他定位技术的比较
| 技术类型 | 基本原理 | 优点 | 缺点 |
|---|---|---|---|
| 多普勒频差定位 | 利用运动产生的频率差 | 无源、作用距离远、精度高 | 依赖目标运动、同步要求高、计算复杂 |
| 到达时间差定位 | 利用信号到达不同接收机的时间差 | 无源、精度高 | 对时间同步要求极高（皮秒级） |
| 到达方向定位 | 利用天线阵列测量信号来波方向 | 无源、设备相对简单、定位速度快 | 需要大型天线阵列、精度受限于基线长度 |
| 信号强度定位 | 利用信号衰减模型 | 简单、成本低 | 精度低、受环境影响大（多径效应） |
多普勒频率差定位技术是一种利用多普勒效应和几何原理进行高精度无源定位的有效手段,它的核心在于通过测量多个静止接收机对运动目标信号频率的微小差异，来构建双曲线定位方程，最终通过解算确定目标位置，尽管它对目标的运动状态和时间同步有严格要求，但在军事侦察、电子战等专业领域，凭借其隐蔽性和高精度，仍然是一种不可或缺的关键技术。
