QPSK调制技术研究报告
摘要
QPSK(Quadrature Phase Shift Keying)是一种在现代数字通信系统中应用极为广泛的关键数字调制技术,它通过在载波的四个不同相位上分别承载二进制比特信息,实现了比BPSK(二进制相移键控)更高的频谱效率,本报告旨在全面深入地研究QPSK调制技术,包括其基本原理、数学表达式、调制解调过程、性能分析(如抗噪声性能、频谱效率),并探讨其优缺点、典型应用以及未来的发展方向。
随着信息时代的到来,对数据传输速率和频谱资源利用效率的要求越来越高,数字调制技术作为连接基带数字信号与适合在信道中传输的带通信号的核心桥梁,其性能直接决定了通信系统的整体表现。
在众多数字调制技术中,相移键控因其对信道的幅度失真不敏感、实现相对简单等优点而备受青睐,QPSK是PSK技术的重要演进,它通过将两个比特(一个符号)映射到一个相位状态,实现了在相同带宽内传输双倍的数据速率,是现代无线通信、卫星通信和有线电视等领域的基石技术之一。
QPSK基本原理
1 核心思想
QPSK的核心思想是将输入的二进制数据流进行分组,每两个比特组成一个“双比特元”(Dibit),为这四种可能的组合(00, 01, 10, 11)分别分配一个独特的相位,这样,每个符号(Symbol)就能携带2个比特的信息。
在一个码元周期内,QPSK信号的相位取自以下四个值之一:
- 0° (或 0 弧度)
- 90° (或 π/2 弧度)
- 180° (或 π 弧度)
- 270° (或 3π/2 弧度)
这种相位图通常被称为星座图,是分析和理解QPSK等调制技术最直观的工具。
2 星座图
QPSK的星座图由四个均匀分布在单位圆上的点组成,相邻点之间的相位差为90°。
- 坐标轴:横轴代表同相分量,纵轴代表正交分量。
- 符号点:每个点代表一个符号,对应一个双比特元。
S₀ = (1, 1)对应00S₁ = (-1, 1)对应01S₂ = (-1, -1)对应11S₃ = (1, -1)对应10
- 欧氏距离:相邻符号点之间的距离(欧氏距离)为
√2,这个距离决定了系统的抗噪声能力,距离越大,抗噪声能力越强。
数学模型与调制过程
1 数学表达式
一个通用的QPSK信号可以表示为:
$$s(t) = A_c \cdot \text{Re}\left[ g(t) \cdot e^{j(2\pi f_c t + \theta_k)} \right]$$
- $A_c$ 是载波振幅。
- $f_c$ 是载波频率。
- $g(t)$ 是成形脉冲,通常为矩形脉冲。
- $\theta_k$ 是第 $k$ 个码元的相位,其取值为 ${0, \pi/2, \pi, 3\pi/2}$。
通过欧拉公式展开,可以得到更常用的同相-正交分量形式:
$$s(t) = A_c \cdot \left[ I_k \cdot \cos(2\pi f_c t) - Q_k \cdot \sin(2\pi f_c t) \right]$$
这里的 $I_k$ 和 $Q_k$ 分别是同相分量和正交分量的幅度值,它们由输入的双比特元决定:
00-> $I_k = +1, Q_k = +1$01-> $I_k = -1, Q_k = +1$11-> $I_k = -1, Q_k = -1$10-> $I_k = +1, Q_k = -1$
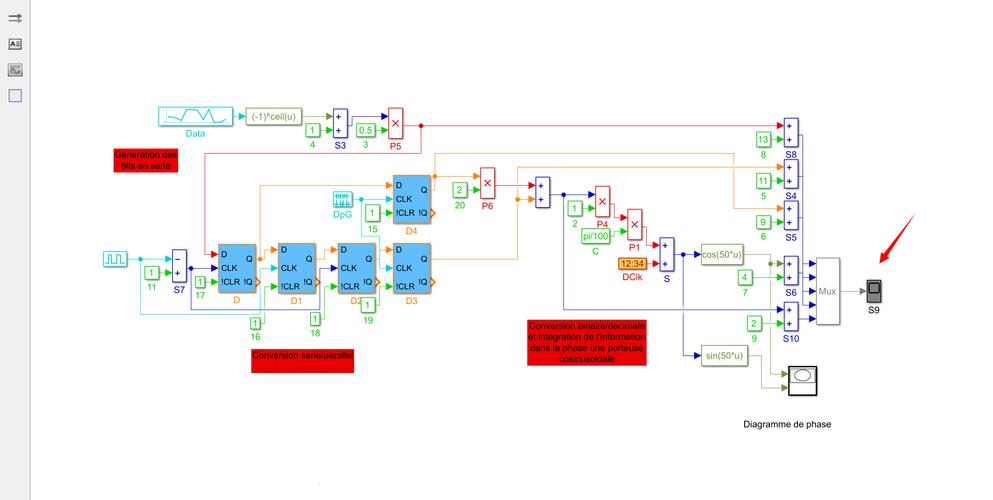
2 调制过程
QPSK的调制过程可以分解为以下几个步骤:
-
串并转换:将高速的串行二进制比特流分成两路并行的低速比特流,一路是同相路,另一路是正交路,输入比特流
1 0 1 1 0 0 ...会被分成:- I路:
1 1 0 ... - Q路:
0 1 0 ... - 这样,每两个时钟周期,I路和Q路各提供一个比特,共同构成一个双比特元。
- I路:
-
电平映射:将并行的两路比特流(I和Q)转换为相应的电平。
- 通常采用双极性不归零信号,比特 '0' 映射为
+1,比特 '1' 映射为-1。
- 通常采用双极性不归零信号,比特 '0' 映射为
-
载波调制:
- 将I路信号与本地载波 $\cos(2\pi f_c t)$ 相乘(进行幅度调制)。
- 将Q路信号与本地载波的移相信号 $-\sin(2\pi f_c t)$ 相乘。
- 注意:两个载波在相位上相差90°,是正交的。
-
信号合成:将调制后的I路信号和Q路信号相加,最终得到QPSK已调信号。
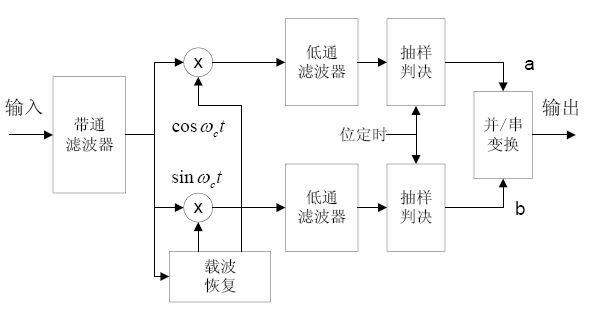
解调过程
QPSK的解调通常采用相干解调,因为它能获得最佳的误码率性能,解调过程是调制的逆过程。
-
载波同步:接收端需要从接收信号中恢复出一个与发送端载波同频同相的本地载波,这是相干解调的关键和难点,通常使用锁相环来实现。
-
正交下变频:
- 将接收信号分别与两个本地正交载波相乘:
- 与 $\cos(2\pi f_c t)$ 相乘,得到同相支路的基带信号。
- 与 $-\sin(2\pi f_c t)$ 相乘,得到正交支路的基带信号。
- 将接收信号分别与两个本地正交载波相乘:
-
积分清除/匹配滤波:对下变频后的信号进行积分或匹配滤波,以在每个码元周期末尾抽样判决,消除码间串扰并提高信噪比。
-
判决与并串转换:
- 判决:对抽样值进行硬判决(或软判决),根据判决门限(通常是0),恢复出原始的比特流。
- 如果I路抽样值 > 0,判为 '0';否则判为 '1'。
- 如果Q路抽样值 > 0,判为 '0';否则判为 '1'。
- 并串转换:将恢复出的两路并行比特流合并成一路串行比特流,从而完成整个解调过程。
- 判决:对抽样值进行硬判决(或软判决),根据判决门限(通常是0),恢复出原始的比特流。
性能分析
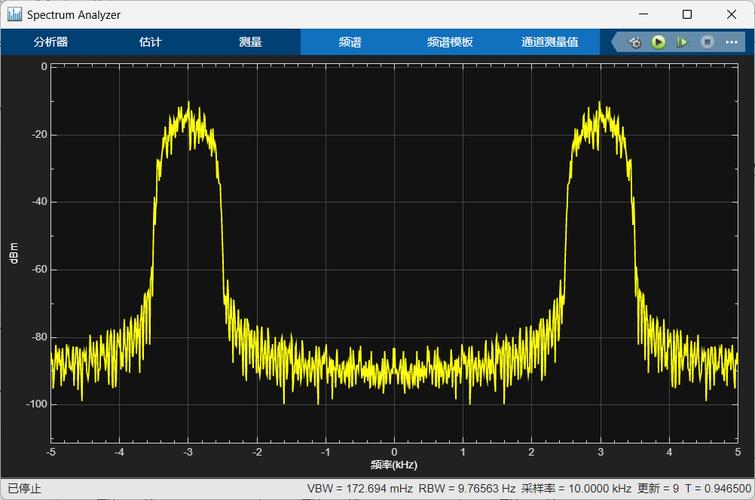
1 频谱效率
频谱效率是衡量调制技术性能最重要的指标之一,单位是 bit/s/Hz。
- 码元速率 ($R_s$):QPSK的码元速率 $R_s$ 等于比特速率 $R_b$ 的一半,因为每个符号携带2个比特。 $$R_s = \frac{R_b}{2}$$
- 最小带宽 ($B_{min}$):对于基带信号,其带宽约为码元速率的2倍(根据奈奎斯特准则),对于带通QPSK信号,其最小带宽为: $$B_{min} = 2 R_s = 2 \times \frac{R_b}{2} = R_b$$
- 频谱效率 ($\eta$): $$\eta = \frac{Rb}{B{min}} = \frac{R_b}{R_b} = 2 \text{ bit/s/Hz}$$
QPSK的频谱效率为 2 bit/s/Hz,这意味着在1Hz的带宽内可以传输2比特的数据,这比BPSK(1 bit/s/Hz)的效率高出一倍。
2 抗噪声性能
抗噪声性能通常用误码率来衡量,在高斯白噪声信道下,QPSK的理论误码率公式为:
$$P_b = Q\left(